DEFINICION
Una función real  es una funcion matematica cuyo domino y codominio están contenidos en el conjunto de los numeros reales denotado como
es una funcion matematica cuyo domino y codominio están contenidos en el conjunto de los numeros reales denotado como  , es decir, es una función:
, es decir, es una función:
Álgebra de las funciones (con valores) reales es una funcion matematica cuyo domino y codominio están contenidos en el conjunto de los numeros reales denotado como
es una funcion matematica cuyo domino y codominio están contenidos en el conjunto de los numeros reales denotado como  , es decir, es una función:
, es decir, es una función:
Sea
 un conjunto cualquiera no vacío y sea
un conjunto cualquiera no vacío y sea  el conjunto formado por todas las funciones de
el conjunto formado por todas las funciones de  en
en  . Muchas de las operaciones y propiedades algebraicas de los números reales se pueden extender a
. Muchas de las operaciones y propiedades algebraicas de los números reales se pueden extender a  , como veremos a continuación.
, como veremos a continuación.Sean
 elementos de
elementos de  . Se definen a continuación operaciones entre esas funciones.
. Se definen a continuación operaciones entre esas funciones.- Suma de funciones:

- Resta de funciones:

- Producto de funciones:

 si y solo si, para todo
si y solo si, para todo  .
.
 . Se indican a continuación aquellas más importantes.
. Se indican a continuación aquellas más importantes.- La suma de funciones es asociativa, conmutativa, y con neutro la función constante
 , con opuesto aditivo
, con opuesto aditivo  para cada función
para cada función  .
. - La resta es tal que
 .
. - La multiplicación es asociativa, conmutativa, y con neutro la función constante
 , pero solamente las funciones que nunca tiene valor nulo tienen recíprocos.
, pero solamente las funciones que nunca tiene valor nulo tienen recíprocos. - La multiplicación es distributuva respecto a la suma.
 . En efecto, supongamos que
. En efecto, supongamos que  y definamos
y definamos  tales que
tales que  y
y  y
y  . Se ve, inmediatamente, que el producto
. Se ve, inmediatamente, que el producto  es la función constante 0, o sea la función cero, aunque ninguno de los factores lo es.
es la función constante 0, o sea la función cero, aunque ninguno de los factores lo es.El conjunto
 junto con sus operaciones es importante por la gran cantidad de ejemplos diversos que se obtienen al seleccionar el conjunto X.
junto con sus operaciones es importante por la gran cantidad de ejemplos diversos que se obtienen al seleccionar el conjunto X.- Sea
 . Entonces, cada función de
. Entonces, cada función de  define una pareja de números
define una pareja de números  que si consideramos el orden natural en X, podemos escribir como el para ordenado
que si consideramos el orden natural en X, podemos escribir como el para ordenado  . Esto nos dice que, en este caso, podemos identificar
. Esto nos dice que, en este caso, podemos identificar  con el conjunto de todos los pares posibles de números reales, o sea con
con el conjunto de todos los pares posibles de números reales, o sea con  .
. - Sea
 Razonado como arriba, podemos identificar a
Razonado como arriba, podemos identificar a  con
con 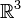 .
. - Sea
 Razonado como arriba, podemos identificar a
Razonado como arriba, podemos identificar a  con
con 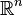 .
.
- Sea
 , el conjunto de los numeros naturales. En este caso,
, el conjunto de los numeros naturales. En este caso,  es el conjunto de todas las sucesiones de números reales provisto como la suma y multiplicación usual de sucesiones.
es el conjunto de todas las sucesiones de números reales provisto como la suma y multiplicación usual de sucesiones.
Las funciones numéricas son funciones cuyo dominio y codominio son subconjuntos de los números reales. Estas funciones son aquellas que aparecen más frecuentemente en las aplicaciones elementales. En el resto del artículo, funciones significará funciones numéricas. Muchas veces, para estas funciones, se da solamente la regla o fórmula de la función. En esa situación se aplica el convenio del dominio natural y se supone que el codominio (natural) consiste de todo
 .
.Funciones acotadas
Se dice que una función
 está acotada cuando su conjunto imagen está acotado. Es decir, hay un número
está acotada cuando su conjunto imagen está acotado. Es decir, hay un número  tal que para todo
tal que para todo  del dominio de la función se cumple que
del dominio de la función se cumple que .
.En forma análoga se define las nociones de función acotada superiormente y función acotada inferiormente, queriendo decir que su conjunto imagen está acotado superiormente o inferiormente respectivamente. Por ejemplo, f(x)=|x| tiene por conjunto imagen
 , está acotada inferiormente.
, está acotada inferiormente.Funciones monótonas
Una función f en un intervalo [a,b] es monótona si verifica cualquiera de las siguientes propiedades:
- es estrictamente creciente,
- si para todo
![x_1, x_2 \in [a,b]: x_1 < x_2](https://upload.wikimedia.org/math/c/1/2/c12f6c1f0a01f1fd1957f6e824c3075a.png) si y solo si
si y solo si  .
.
- si para todo
- es estrictamente decreciente,
- si para todo
![x_1, x_2 \in [a,b]: x_1 < x_2](https://upload.wikimedia.org/math/c/1/2/c12f6c1f0a01f1fd1957f6e824c3075a.png) si y solo si
si y solo si  .
.
- si para todo
- es creciente,
- si para todo
![x_1, x_2 \in [a,b]: x_1 < x_2](https://upload.wikimedia.org/math/c/1/2/c12f6c1f0a01f1fd1957f6e824c3075a.png) si y solo si
si y solo si  .
.
- si para todo
- es decreciente,
- si para todo
![x_1, x_2 \in [a,b]: x_1 < x_2](https://upload.wikimedia.org/math/c/1/2/c12f6c1f0a01f1fd1957f6e824c3075a.png) si y solo si
si y solo si  .
.
- si para todo
- Si una función es estrictamente creciente o decreciente entonces es inyectiva
- La suma de funciones monótonas de un mismo tipo tiene el mismo tipo de monotonía. Lo anterior no se verifica ni para restas ni para productos.
Una función es par cuando presenta simetría sobre el eje
 , esto es, si para todo elemento
, esto es, si para todo elemento  de su dominio se cumple que
de su dominio se cumple que 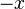 también está en el dominio y
también está en el dominio y
 de su dominio se cumple que
de su dominio se cumple que 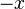 también está en el dominio y
también está en el dominio y
Propiedades
- La suma de dos funciones pares o dos funciones impares es par.
- El producto de función par por par o impar por impar, da par.
- Todas las otras combinaciones dan impar.
Decimos función es periódica si se cumple:
 donde
donde 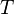 es un periodo de la función. El periodo es el menor de los periodos positivos, cuando exista tal número.
es un periodo de la función. El periodo es el menor de los periodos positivos, cuando exista tal número.Los ejemplos clásicos son las funciones seno y coseno con periodos iguales a
 . Si int denota la funcion parte entera (que produce el mayor entero menor o igual al argumento) entonces la función
. Si int denota la funcion parte entera (que produce el mayor entero menor o igual al argumento) entonces la función  tal que
tal que  tiene periodo 1.
tiene periodo 1.Una función es periódica alternada cuando se cumple:
 .
Estas últimas también son conocidas como funciones simétricas de media
onda y constan de dos semiondas iguales de sentidos opuestos.
.
Estas últimas también son conocidas como funciones simétricas de media
onda y constan de dos semiondas iguales de sentidos opuestos.Funciones cóncavas y convexas

MAS INFORMACION:http://es.slideshare.net/nivelacion008/cap-9-funcion-de-una-variable-real?related=2

No hay comentarios:
Publicar un comentario