8.1 AXIOMAS DE PEANO
8.2 INDUCCIÓN MATEMÁTICA
8.3 FACTORIAL
8.4 TEOREMA DEL BINOMIO
8.5 SUCESIONES ARITMÉTICAS Y GEOMÉTRICAS
AXIOMAS DE PEANO
Los cinco axiomas o postulados de Peano son los siguientes:
- El 1 es un número natural.1 está en N, el conjunto de los números naturales.
- Todo número natural n tiene un sucesor n* (este axioma es usado para definir posteriormente la suma).
- El 1 no es el sucesor de algún número natural.
- Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
- Si el 1 pertenece a un conjunto K de números naturales, y dado un
elemento cualquiera k, el sucesor k* también pertenece al conjunto K,
entonces todos los números naturales pertenecen a ese conjunto K. Este
último axioma es el principio de induccion matematica
Los cinco axiomas de Peano son:
INDUCCION MATEMATICA
En matematicas, la inducción es un razonamiento que permite demostrar proposisciones que dependen de una variable
 que toma una infinidad de valores enteros En términos simples, la inducción matemática consiste en el siguiente razonamiento:
que toma una infinidad de valores enteros En términos simples, la inducción matemática consiste en el siguiente razonamiento:- El número entero
 tiene la propiedad
tiene la propiedad  . El hecho de que cualquier número entero
. El hecho de que cualquier número entero  también tenga la propiedad
también tenga la propiedad  implica que
implica que  también la tiene. Entonces todos los números enteros a partir de
también la tiene. Entonces todos los números enteros a partir de  tienen la propiedad
tienen la propiedad  .
.
 a la proposición, donde
a la proposición, donde  es el rango.
es el rango.- Base- Se demuestra que
 es cierta, esto es el primer valor que cumple la proposición (iniciación de la inducción).
es cierta, esto es el primer valor que cumple la proposición (iniciación de la inducción). - Paso inductivo- Se demuestra que si
 es cierta, esto es, como hipótesis inductiva, entonces
es cierta, esto es, como hipótesis inductiva, entonces  lo es también, y esto sin condición sobre el entero natural
lo es también, y esto sin condición sobre el entero natural  (relación de inducción. Indicado como
(relación de inducción. Indicado como  ).
).
 es cierto para todo natural
es cierto para todo natural  .
.La inducción puede empezar por otro término que no sea
 , digamos por
, digamos por  . Entonces
. Entonces  será válido a partir del número
será válido a partir del número  , es decir, para todo natural
, es decir, para todo natural  .
.Ejemplo
Se probará que la siguiente declaración P ( n ), que se supone válida para todos los números naturales n .
Base: Se muestra que es válida para n = 0.
con P(0) se tiene:
mientras que el término derecho, 0·(0 + 1)/2 = 0.
Ambos lados son iguales, n = 0. Entonces P(0) es verdadera.
Paso inductivo: Mostrar que si P(k) es verdadera, entonces P(k + 1) es verdadera. Como sigue:
Se asume que P(k) es verdadera (para un valor no específico de k). Se debe entonces mostrar que P(k + 1) es verdadera:
El factorial de un entero positivo n, el factorial de n o n factorial se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los numeros naturales) hasta n. Por ejemplo,
La función factorial es formalmente definida mediante el producto
 .
.
 .
.
Todas las definiciones anteriores incorporan la premisa de que
TEOREMA DEL BINOMIO
En matematica, el teorema del binomio es una fórmula que proporciona el desarrollo de la potencia n-ésima de n (siendo n, entero positivo) de un binomio. De acuerdo con el teorema, es posible expandir la potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son numero natural con b + c = n, y el coeficiente a de cada término es un numero entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
Como ejemplo, para n=2, n=3, n=4, utilizando los coeficientes del triangulo de pascal:
Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en los términos con potencias impares de y. La expresión (2) queda de la siguiente forma:
Teorema generalizado del binomio (Newton)
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:Donde r puede ser cualquier numero real (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por:
Una forma útil pero no obvia para la potencia recíproca:
SUCESIONES ARITMICAS Y GEOMETRICAS
Progresiones aritméticas
Una progresión aritmética es una sucesión de números tales que cada uno de ellos (salvo el primero) es igual al anterior más un número fijo llamado diferencia que se representa por d.
Diferencia
d = an - an-1
Término general de una progresión aritmética
an = a1 + (n - 1) · d
an = ak + (n - k) · d
Interpolación de términos
Sean los extremos a y b, y el número de medios a interpolar m.

Suma de términos equidistantes
ai + aj = a1 + an

a3 + an-2 = a2 + an-1 = a1 + an
Suma de n términos consecutivos

Progresiones geométricas
Una progresión geométrica es una sucesión en la que cada término se obtiene multiplicando al anterior una cantidad fija r, llamada razón.

Término general de una progresión geométrica
an = a1 · rn-1
an = ak · rn-k
Interpolación de términos

Suma de n términos consecutivos

Suma de los términos de una progresión geométrica decreciente

Producto de dos términos equidistantes
ai . aj = a1 . an

a3 · an-2 = a2 · an-1 = ... = a1 · an
Producto de n términos equidistantes

MAS INFORMACION: http://es.slideshare.net/nivelacion008/cap-8-numeros-naturales?related=1















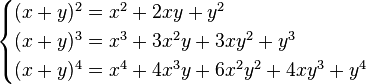
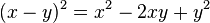
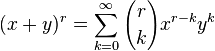
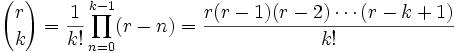

No hay comentarios:
Publicar un comentario