6.1 INTERVALOS
6.2 VALOR ABSOLUTO
6.3 ECUACIONES EN UNA INCOGNITA
• ECUACIONES LINEALES
• ECUACIONES CUADRÁTICAS
• ECUACIONES CON RADICALES
• ECUACIONES CON VALOR ABSOLUTO
• PROBLEMAS.
INTERVALOS
Intervalo abierto
No incluye los extremos.
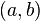 o bien
o bien ![]a,b[\](https://upload.wikimedia.org/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)
- Notación conjuntista o en términos de desigualdades:
En la topología usual de la recta (o ℝ) se usa un intervalo abierto para definir un conjunto abierto en dicha topología. En la topología usual de ℝ, un intervalo abierto es un conjunto abierto. El intervalo abierto <a, b> es igual a su interior, su frontera es el conjunto {a, b} y su clausura es el intervalo cerrado [a, b].No tiene puntos aislados, mientras que todos su puntos son puntos de acumulación del mismo intervalo, de suma importancia en asuntos de límites de funciones
Intervalo cerrado
Sí incluye los extremos.
- Que se indica:
![I = [a,b]\](https://upload.wikimedia.org/math/5/a/6/5a6aef6ce626a63d1e3c1cfb17e1a97e.png)
- Con la notación
![(a,b]\](https://upload.wikimedia.org/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](https://upload.wikimedia.org/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) indicamos.
indicamos.
- Y con la notación
 o bien
o bien 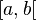 ,
,
Los intervalos finitos tienen un centro de simetría que es (a + b)/2, llamado punto medio, donde los extremos son a y b con a < b. En el caso a=b, no existe punto medio y el intervalo abierto es ∅
Intervalo infinito
Incluye un extremo e infinito por la derecha.
- Con la notación
 indicamos.
indicamos.
- Y con la notación
 ,
,
- Con la notación
![(-\infty, a]\](https://upload.wikimedia.org/math/0/7/b/07bb1e1c13ff67945983bf469caffc2e.png) indicamos.
indicamos.
- Y con la notación
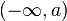 ,
,
- Y con la notación
 ,
,
VALOR ABSOLUTO
Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia desde ese número al origen.
 |
Observe en el dibujo que la distancia del 6 al origen es 6 unidades, igualmente la distancia del punto −6 al origen es 6. En notación, esto es |−6| = 6.
Las barras se leen como el valor absoluto de lo que esta dentro de ellas.
En el valor absoluto no importa en que lado de la recta real está representado el número.
De modo general, el valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo o cero, y opuesto de a, si a es negativo.
Analíticamente podemos ver que si a es positivo, es decir esta a la derecha del cero, entonces |a| = a y si está a la izquierda del origen, es decir si a es negativo, entonces |a| = −a.
Formalmente, el valor absoluto o módulo de todo número real |a| está definido por:
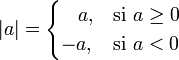
Desde un punto de vista geométrico, el valor absoluto de un número real |a| es siempre positivo o cero, pero nunca negativo.
En general, el valor absoluto de la diferencia de dos números reales |a − b| es la distancia entre ellos.
Veamos los siguientes ejemplos
Ejemplo 1
a)
b)
Observe como el valor absoluto a una cantidad positiva la deja igual y a una cantidad negativa le cambia el signo.
c) Si x > 2 entonces | x – 2| = x – 2, pues x − 2 > 0. Dicho de otra manera, si la expresión a la que le estamos tomando valor absoluto es de signo positivo, el valor absoluto la deja igual.
d) Si x < 2 entonces |x – 2| = – (x – 2), pues x − 2 < 0 . Dicho de otro modo, si la expresión a la que le estamos tomando valor absoluto es de signo negativo, el valor absoluto la cambia de signo.
ECUACIONES CON UNA INCOGNITA
ECUACIONES LINEALES
Solución de una
ecuación lineal
Cualquier conjunto
de n números reales que verifica la ecuación se denomina solución de la
ecuación.
Dada la ecuación x
+ y + z + t = 0, son soluciones de ella:
(1,-1,1,-1),
(-2,-2,0, 4).
Ecuaciones
lineales equivalentes
Son aquellas que
tienen la misma solución.
x + y + z + t = 0
2x + 2y + 2z + 2t = 0
ECUACIONES CUADRATICAS
Una ecuación
cuadrática es una ecuación en su forma ax2 + bx + c, donde a, b, y c son números reales.
Ejemplo:
9x2 + 6x + 10 a = 9, b = 6, c = 10
3x2 - 9x a = 3, b = -9, c = 0
-6x 2 + 10 a = -6, b = 0, c = 10
ECUACIONES CON RADICALES
Las ecuaciones
con radicales son aquellas que tienen la x dentro de raices cuadradas. Para
solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado
para eliminarlas.
Al elevar al
cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso,
al finalizar, hay que hacer la comprobación en la ecuación inicial para
detectar y recharzar las que no sean válidas.
Ejemplo: Ecuaciones con radicales
Resuelve las ecuaciones:
-
- a)
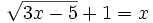
- a)
-
- b)
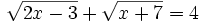
- b)
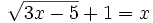
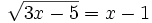
Se elevan al cuadrado los dos lados de la ecuación:
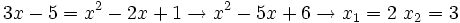
Comprobación:
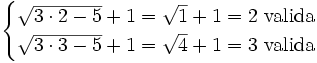
a)
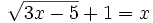
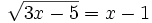
Se elevan al cuadrado los dos lados de la ecuación:
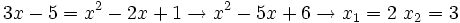
Comprobación:
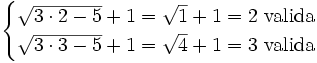
ECUACIONES CON VALOR ABSOLUTO
Una expresión que
está dentro de las barras de valor absoluto puede ser más complicada que
una simple variable, Cuando éstas expresiones incluyen otros valores y
operaciones, debemos tener mucho cuidado, especialmente cuando
resolvemos sus opuestos.
Para resolver |-2x| = 8, por ejemplo, debemos considerar dos posibilidades — que la expresión dentro de las barras de valor absoluto, -2x, sea positiva o negativa.
Si la expresión -2x es positiva, entonces
-2x = 8
Para resolver x, podemos dividir entre -2 cada lado de la ecuación y obtenemos
x = -4
Si la expresión -2x es negativa, entonces
-(-2x) = 8
Para resolver x, multiplicamos -2x por -1 y obtenemos
2x = 8
Luego dividimos cada lado de la ecuación entre 2 para obtener
x = 4
Entonces, la solución de |-2x| = 8 es
x = -4, 4
MAS INFORMACION: http://es.slideshare.net/nivelacion008/cap-6-ecuaciones



![I = [a,b], \quad
\forall x \in I: \quad a \le x \le b](https://upload.wikimedia.org/math/f/0/e/f0eab172bfb0ca73e44d6c3ba25bdb9b.png)

![I = (a,b], \quad
\forall x \in I: \quad a < x \le b](https://upload.wikimedia.org/math/1/7/1/1719859fa355ba4d195ddbaf9f242697.png)

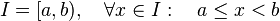

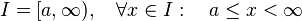



![I = (-\infty, a], \quad
\forall x \in I: \quad x \le a < \infty](https://upload.wikimedia.org/math/1/7/8/17865270392a210f1638622881480693.png)




No hay comentarios:
Publicar un comentario