15.1 DISTANCIA ENTRE DOS PUNTOS
15.2 CIRCUNFERENCIA
15.3 PROBLEMAS DE APLICACIÓN
DISTANCIA ENTRE DOS PUNTOS
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1) .
Ejemplo:
La distancia entre los puntos (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Para demostrar esta relación se deben ubicar los puntos P1(x1, y1) y P2(x2, y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa P1P2 y emplear el Teorema de Pitagoras
Ejemplo:
Calcula la distancia entre los puntos P1(7, 5) y P2(4, 1)
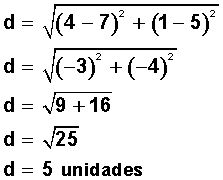
Sean P1 (x1, y1) y P2 (x2, y2) dos puntos en el plano.
La distancia entre los puntos P1 y P2 denotada por d =
En la Figura 1 hemos localizado los puntos P1 (x1, y1) y P2 (x2, y2) así como también el segmento de recta 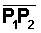
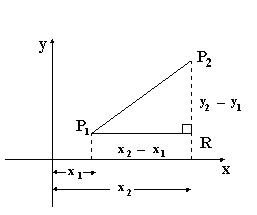 |
Figura 1
Al trazar por el punto P1 una paralela al eje x (abscisas) y por P2 una paralela al eje y (ordenadas), éstas se interceptan en el punto R, determinado el triángulo rectángulo P1RP2 y en el cual podemos aplicar el Teorema de Pitagoras
Al trazar por el punto P1 una paralela al eje x (abscisas) y por P2 una paralela al eje y (ordenadas), éstas se interceptan en el punto R, determinado el triángulo rectángulo P1RP2 y en el cual podemos aplicar el Teorema de Pitagoras
CIRCUNFERENCIA
En un sistema de coordenas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuacion
 .
.
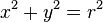 .
.
De la ecuación general de una circunferencia,
 ,
,la ecuación de la circunferencia es:
MAS INFORMACION: http://es.slideshare.net/nivelacion008/c-ap15-circunferencia
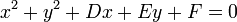




No hay comentarios:
Publicar un comentario