14.1 Definición
14.2 Método
de Gauss
14.3 Representación
Matricial
METODO GAUSS
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
son las incógnitas y los números 
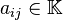son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png)
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
MAS INFORMACION:http://es.slideshare.net/nivelacion008/cap14-siste-linel?related=3
DEFINICION
En matematicas y algebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal,
es un conjunto de ecuaciones lineales (es decir, un sistema de
ecuaciones en donde cada ecuacion es de primer grado), definidas sobre
un cuerpo o un anillo conmutativo Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
METODO GAUSS
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
Eliminación de Gauss-Jordan
Una variante de este método, denominada eliminacion de Gauss-Jordan , es un método aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en triangular la matriz aumentadadel sistema mediante transformaciones elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será igual al coeficiente situado en la misma fila de la matriz. Este procedimiento es similar al anterior de reducción, pero ejecutado de manera reiterada y siguiendo un cierto orden algorítmico.Regla de Cramer
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
REPRESENTACION MATRICIAL
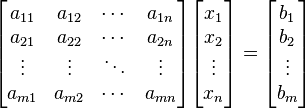
En general, un sistema con m ecuaciones lineales y n incognitas puede ser escrito en forma normal como:Donde
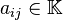son las incógnitas y los números son los coeficientes del sistema sobre el cuerpo . Es posible reescribir el sistema separando con coeficientes con notación matricial:Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cierpo del que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este sistema lineal. A b se le llama vector de términos independientes del sistema y a x se le llama vector de incógnitas.
MAS INFORMACION:http://es.slideshare.net/nivelacion008/cap14-siste-linel?related=3
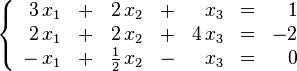
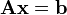
No hay comentarios:
Publicar un comentario