2.1 DEFINICION
2.2 NOTACION
2.3 CARDINALIDAD
2.4 REPRESENTACION GRAFICA
2.5 IGUALDADES
2.6 SUBCONJUNTOS
2.7 OPERACIONES
2.8 ALGEBRA DE CONJUNTOS
DEFINICIÓN
Un CONJUNTO es una agrupación bien definida de objetos
llamados elementos.
NOTACIÓN
Para denotar a un
conjunto usualmente se emplean las primeras letras del abecedario, en
mayúscula.
Podemos referirnos
a un conjunto indicando cada uno de sus elementos.
Ejemplo
Si queremos
referirnos al conjunto de las vocales, se lo puede hacer nombrando a cada
vocal, es decir:
Esta manera de
referirnos a los conjuntos se denomina por extensión o tabulación.
También podemos
referirnos a un conjunto indicando las características de sus elementos.
Ejemplo
Podemos referirnos
al conjunto de las vocales de esta otra forma:
Esta otra forma de
referirnos a un conjunto se denomina por comprensión
Esto último se
hace necesario cuando un conjunto tiene muchos elementos.
CARDINALIDAD
REPRESENTACIÓN GRÁFICA
A los conjuntos se
los suele representar gráficamente mediante los llamados DIAGRAMA DE VENN.
IGUALDAD
Dos conjuntos A y
B son iguales si ambos tienen los mismos elementos. En este caso, se denota
A=B. Escribimos A?B si los conjuntos no tienen los mismos elementos.
Consideremos los conjuntos.
A= {x/x letras de
la palabra arma} yB={x/x letras de la palabra rama}
CONJUNTOS DISYUNTOS.
Dos conjuntos A y
B son Disyuntos si y sólo si, no tienen
elementos en común. Es decir, son conjuntos diferentes, “A” NO ES IGUAL A “B”
Gráficamente tenemos:
SUBCONJUNTOS
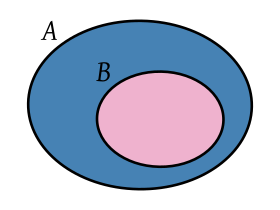

Subconjunto. B es un subconjuntode A (en particular un subconjunto propio).
Un subconjunto A de un conjunto
B, es un conjunto que contiene algunos de los elementos de B (o
quizá todos):
Un conjunto A es
un subconjunto del conjunto B si cada elemento de A es a su vez
un elemento de B.
|
Cuando A es un subconjunto de B,
se denota como A ⊆ B y se dice
que «A está contenido en B». También puede escribirse B ⊇ A, y decirse que B es un superconjunto
de A y también «B contiene a A» o «B incluye a A».
Todo conjunto A es un
subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de A
es a su vez un elemento de A». Es habitual establecer una distinción más
fina mediante el concepto de subconjunto propio: A es un subconjunto
propio de B si es un subconjunto de B pero no es igual a B.
Se denota como A ⊊ B, es decir: A
⊆ B pero A ≠ B (y
equivalentemente, para un superconjunto propio, B ⊋ A).
Ejemplos.
El «conjunto de todos los hombres» es
un subconjunto propio del «conjunto de todas las personas».
{1, 3} ⊊ {1, 2,
3, 4}
{1, 2, 3, 4} ⊆ {1, 2, 3, 4}
Conjuntos
disjuntos
Dos conjuntos A y B son
disjuntos si no tienen ningún elemento en común. Por ejemplo, los conjuntos de
los numeros racionales
y los numeros irracionales
son disjuntos: no hay ningún número que sea a la vez racional e irracional. La intersecion de dos conjuntos disjuntos es el conjunto vacío.
OPERACIONES
OPERACIONES
Existen varias
operaciones básicas que pueden realizarse para, partiendo de ciertos conjuntos
dados, obtener nuevos conjuntos:
Unión: (símbolo ∪) La union de dos conjuntos A y B, que se representa como A ∪ B, es el conjunto de todos
los elementos que
pertenecen al menos a uno de los conjuntos A y B.
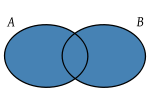

Intersección: (símbolo ∩) La interseccion de dos conjuntos A y B es el
conjunto A ∩ B de los elementos comunes a A y B.


Diferencia: (símbolo \) La diferencia del conjunto A con B es el
conjunto A
\ B que resulta de
eliminar de A
cualquier elemento que esté en B.


Complemento: El complemento de un conjunto A es el
conjunto A∁
que contiene todos los elementos que no pertenecen a A, respecto a un conjunto U que lo
contiene.


Diferencia
simétrica: (símbolo Δ) La diferencia simetrica de dos conjuntos A y B es el
conjunto A
Δ B con todos los
elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.


Producto
cartesiano: (símbolo ×) El producto cartesiano de dos conjuntos A y B es el
conjunto A
× B de todos los pares ordenados (a,
b) formados con un
primer elemento a
perteneciente a A,
y un segundo elemento b perteneciente a B.

No hay comentarios:
Publicar un comentario