17.1 ANGULOS OPUESTOS POR EL VÉRTICE
17.2 ANGULOS ALTERNOS INTERNOS, ALTERNOS EXTERNOS,
CORRESPONDIENTES.
17.3 FIGURA PLANA.
17.4 TRIÁNGULOS.
17.5 CUADRILATEROS.
17.6 FIGURAS CIRCULARES
ANGULOS OPUESTOS POR EL VERTICE
En la figura los ángulos a, c y b, d son opuestos por el vértice. Dos ángulos opuestos por el vértice son congruentes
ANGULOS ALTERNOS INTERNO, ALTERNOS EXTERNOS,CORRESPENDIENTES
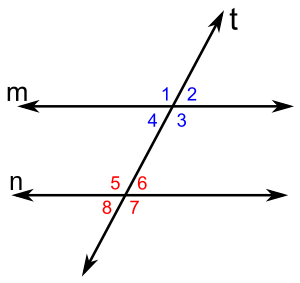
Las parejas de ángulos: <1 y <5; <2 y <6; <4 y <8; <3 y <7 se llaman ángulos correspondientes, y son congruentes (figura 1).
== Ángulos alternos == Son los que "fuera" de las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.
Alternos externos
Las parejas de ángulos: <1 y <7; <2 y <8 se llaman ángulos alternos externos, y son congruentesAlternos internos
Las parejas de ángulos: <4 y <6; <3 y <5 se llaman ángulos alternos internos, y son congruentesFIGURA PLANA
Poligonal:
Definida por todos los puntos del plano que pertenecen a la frontera de
la figura plana.
La poligonal
divide al plano en dos regiones: la interior a la poligonal y la exterior a la
poligonal.
Polígono:
Definido por todos los puntos del plano que pertenecen tanto a lo
poligonal como a la región interior de la poligonal.
Si los lados del
polígono son de igual medida, se dice que es un polígono regular; caso
contrario se dice que es un polígono irregular.
Trataremos ciertos
polígonos de interés.
TRINAGULOS
- Como triangulo equilatero cuando los tres lados del triángulo tienen una misma longitud (los tres angulos internos miden 60 grados o
 radiantes).
radiantes).
- Como triángulo isósceles (del griego ἴσος "igual" y σκέλη "piernas", es decir, "con dos piernas iguales"), si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. Un triángulo es isósceles cuando tiene dos lados iguales; esto no descarta que los tres lados sean iguales, de modo que todo triángulo equilátero sea isósceles, pero no se cumple el enunciado recíproco.
A + 2B = A +2C = 180º;
A' + 2B' = A' + 2C' = 360º; A' = 2C = 2B; B'=C'=A+B= A+C
 donde
donde  son la mediana, altura del lado lado a y bisectriz de su ángulo A opuesto.
son la mediana, altura del lado lado a y bisectriz de su ángulo A opuesto. - Como triángulo escaleno (del griego σκαληνός "desigual"), si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).
 |
 |
 |
| Equilátero | Isósceles | Escaleno |
CUADRILATEROS
Los cuadriláteros son polígonos de cuatro lados.
La suma de los ángulos interiores de un cuadrilátero es igual a 360°.
Clasificación de cuadriláteros
1 Paralelogramos: Cuadriláteros que tienen los lados paralelos dos a dos. Se clasifican en:
Cuadrado
Tiene los 4 lados iguales y los 4 ángulos rectos.
Rectangulo
Tiene lados iguales dos a dos y los 4 ángulos rectos.
Rombo
Tiene los cuatro lados iguales.
Romboide
Tiene lados iguales dos a dos.
Trapecio isósceles
Tiene dos lados no paralelos iguales.
MAS INFORMACION:http://es.slideshare.net/nivelacion008/cap17-geometria-plana?related=2


No hay comentarios:
Publicar un comentario