MATEMATICAS: CAPITULO 16

CAP 16 FUNCIONES TRIGONOMETRICAS

16.1 Angulo

16.2 Función Seno y Función Coseno

16.3 Función Tangente

16.4 Valores de Funciones Trigonométricas para ángulos conocidos

16.5 Identidades Trigonométricas

ANGULO

Un ángulo es la región del plano comprendida entre dos semirrectas con origen común.
A las semirrectas se las llama lados y al origen común vértice.

Medición de ángulos

Para medir ángulos utilizamos el grado sexagesimal (°)
Grado sexagesimal es la amplitud del ángulo resultante de dividir la circunferencia en 360 partes iguales.

1º = 60' = 3600''

1' = 60''

Radián

Radián (rad) es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.

1 rad= 57° 17' 44.8''

360º = 2π rad

FUNCION SENO Y FUNCION COSENO

Funcion seno

La función seno asocia a cada número real, x, el valor del seno del ángulo cuya medida en radianes es x.

f(x) = sen x

Propiedades de la función seno

Dominio: Erre

Recorrido: [-1, 1]

Período: 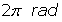Propiedades

Continuidad: Continua en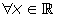

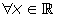
Creciente en: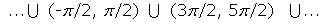

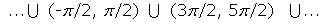
Decreciente en: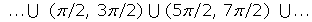

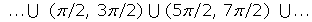
Máximos: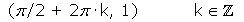

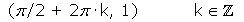
Mínimos: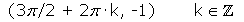

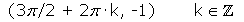
Impar: sen(-x) = -sen x

Cortes con el eje OX: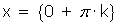

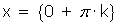
Funcion coseno

La función coseno asocia a cada número real, x, el valor del coseno del ángulo cuya medida en radianes es x.

f(x) = cosen x

Propiedades de la función coseno

Dominio: Erre

Recorrido: [-1, 1]

Período: 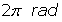Propiedades

Continuidad: Continua en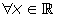

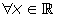
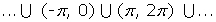
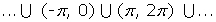
Creciente en: Propiedades

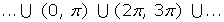
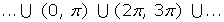
Decreciente en: Propiedades

Máximos: Propiedades

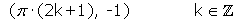
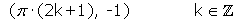
Mínimos: Propiedades

Par: cos(-x) = cos x

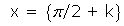
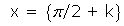
Cortes con el eje OX: Propiedades

FUNCION TANGENTE

La función tangente asocia a cada número real, x, el valor de la tangente del ángulo cuya medida en radianes es x.

f(x) = tg x

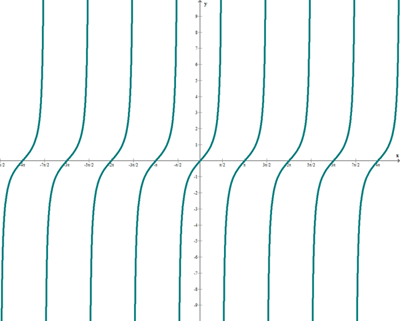
Propiedades de la función tangente

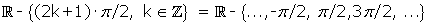
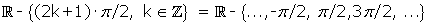
Dominio: Propiedades

Recorrido: Erre

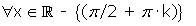
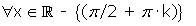
Continuidad: Continua en Propiedades

Período: Propiedades

Creciente en: Erre

Máximos: No tiene.

Mínimos: No tiene.

Impar: tg(−x) = −tg x

Cortes con el eje OX:

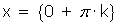
FUNCIONES DE VALORES TRIGONOMETRICAS POR ANGULOS CONOCIDOS

Con ciertos ángulos el estudiante puede concebir estrategias básicas para solucionar situaciones prácticas. Para otros ángulos no nos preocuparemos mayormente, porque bastará sólo con emplear una calculadora.

Ubiquemos en una tabla los valores del seno, coseno y tangente para los ángulos que ya definimos anteriormente y además también para los ángulos de 30°, 45° y 60°, que justificaremos luego.

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo:

\alpha

, del vértice A, se parte de un triangulo rectanguloarbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo $\alpha$ .
El cateto adyacente (b) es el lado adyacente al ángulo $\alpha$ .

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radiantes (5 o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sen \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo

\alpha

, en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}$

IDENTIDADES TRIGONOMETRICAS

Sabiendo las funciones trigonométricas de la suma de dos ángulos, se pueden determinar las funciones trigonométricas de ángulo doble al plantear que

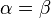
\alpha = \beta

$\sen(\alpha+\beta) =\sen \alpha \cos \beta + \sen \beta \cos \alpha$
$\sen 2\alpha =\sen\alpha \cos\alpha + \sen\alpha\cos\alpha = 2\sen\alpha\cos\alpha$
$\cos(\alpha+\beta)=cos \alpha \cos\beta-\sen\alpha\sen\beta$
$\cos 2\alpha = \cos^2\alpha-\sen^2\alpha$