10.1 Función Exponencial
10.2 Función Logarítmica
10.3
Propiedades de los Logarítmos
10.4 Ecuaciones Exponenciales
10.5 Ecuaciones Logarítmicas.
FUNCION EXPONENCIAL
La función exponencial, es conocida formalmente como la funcion real ex, donde e es el numero de Euler, aproximadamente 2.71828...; esta función tiene por domino de definicion el conjunto de los numeros reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la funcion inversa del logartimo natural
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R numeros reales con a > 0, a ≠ 1. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen. La que se estudia en cursos básicos es


Función logarítmica
Para justificar la definición de logaritmos, es necesario mostrar que la ecuacion exponencialtiene una solución x y que esta solución es única, provista de que y es positivo y que b es positivo y distinto de 1. Una demostración de este hecho requiere del teorema del valor intermedio del calculo elemental.7 Este teorema establece que una funcion continua que produce dos valores m y n también produce cualquier valor que se encuentre entre m y n. Una función es continua si esta no «salta», esto es, si su gráfico puede ser escrito sin levantar el lápiz del papel.
Esta propiedad se puede demostrar que se cumple para la función f(x) = bx. Puesto que f toma arbitrariamente valores grandes positivos y valores pequeños positivos, cualquier número y > 0 que se encuentra entre f(x0) y f(x1) para un adecuado x0 y x1. Por lo tanto, el teorema del valor intermedio asegura que la ecuación f(x) = y tiene una solución. Más aún, hay únicamente una solución para esta ecuación, puesto que la función f es estrictamente creciente (para b > 1), o estrictamente decreciente (para 0 < b < 1).
La única solución x es el logaritmo de y en la base b, logb(y). La función que asigna a cada y su logaritmo se llama función logaritmo o función logarítmica (o logaritmo a secas).
Propiedades de los logaritmos
1. El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

Ejemplo


2. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:

Ejemplo


3. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:

Ejemplo


4.El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:

Ejemplo


5. Cambio de base:

Ejemplo

ECUACION EXPONENCIAL
Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.
Para resolver una ecuación exponencial vamos a tener en cuenta:
1.

2.

3. Las propiedades de las potencias.
a0 = 1
a1 = a


am · a n = am+n
am : a n = am - n
(am)n = am · n
an · b n = (a · b) n
an : b n = (a : b) n
Resolución de ecuaciones exponenciales
Caso 1

Ejemplos





1. 


2. 


3. 




Caso 2

Ejemplo






Caso 3
Ejemplos
 Posteriormente realizamos el cambio de variable:
Posteriormente realizamos el cambio de variable:
 Resolvemos la ecuación y deshacemos el cambio de variable.
Resolvemos la ecuación y deshacemos el cambio de variable.















1. 
En primer lugar aplicamos las propiedades de las potencias del
producto o el cociente, para quitar las sumas o restas de los
exponentes.



2. 







3. 




Deshacemos el cambio de variable en primer con el signo más.

Como no podemos igualar exponentes tomamos logaritmos en los dos miembros y en el primer miembro aplicamos la propiedad:


Despejamos la x

Con el signo negativo no tendríamos solución porque
al aplicar logaritmos en el segundo miembro nos encontraríamos con el
logaritmo de un número negativo, que no existe.

Caso 4






Ecuación logarítmica
Las ecuaciones logarítmicas son aquellas ecuaciones en la que la incógnita aparece afectada por un logaritmo
Para resolver ecuaciones logarítmicas vamos a tener en cuenta:
1Las propiedades de los logaritmos.1

2

3

4

5

6

7

2inyectividad del logaritmo:


Ejemplos
1.

En el primer miembro aplicamos del logaritmo de un producto y en segundo la propiedad del logaritmo de una potencia.

Teniendo en cuenta la inyectividad de los logartmos tenemos:

Resolvemos la ecuación y comprobamos que no obtenemos un logartmo nulo o negativo.




En el 2º miembro aplicamos la propiedad del logaritmo de un cociente.

Restamos en los dos miembros log x y teniedo en cuenta que el log 10 = 1, tenemos:

Teniendo en cuenta la definición de logaritmo y que es un logaritmo decimal:


En primer miembro aplicamos la propiedad del producto y en el 2º la de la potencia de un logaritmo.

Teniendo en cuenta la inyectividad de los logartmos tenemos:

Resolvemos la ecuación y comprobamos la solución.


Multiplicamos en los dos miembros por log(3x −4).

En el 2º miembro aplicamos la propiedad de la potencia de un logaritmo y tenemos en cuenta la inyectividad de los logartmos.

Resolvemos la ecuación x = 0 no es solución
porque nos encontrariamos al sustituir en la ecuación nos encontraríamos
en el denominador un logarítmo negativo.

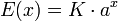

No hay comentarios:
Publicar un comentario