CAP 4 RELACIONES Y FUNCIONES
4.1 PARES ORDENADOS
4.2 PRODUCTO CARTESIANO
4.3 REPRESENTACION
4.4 RELACIONES
4.1 PARES ORDENADOS
Cuando hablamos de par ordenado, nos estamos refiriendo a dos números, o figuras, encerrados en un paréntesis.
Su representación general es:
( a , b )
Respecto a esto, podemos preguntarnos ¿cómo se obtiene un par ordenado?, ¿para qué sirve un par ordenado?
Un par ordenado se puede obtener desarrollando una función o realizando la operación llamada producto cartesiano.
Como consecuencia, un par ordenado sirve para representar un subconjunto del producto cartesiano entre dos conjuntos, un punto en un plano cartesiano o bien una razón o una función.
4.2 PRODUCTO CARTESIANO
Cada par ordenado es una combinación entre elementos del conjunto A y elementos del conjunto B. Siempre el primer elemento pertenece al primer conjunto y el segundo elemento al segundo conjunto pero no al revés porque su representación no es conmutativa, es decir, no se puede alterar el orden.
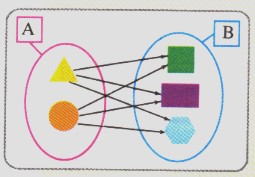
Observa en el recuadro los conjuntos A y B y las combinaciones que se pueden hacer entre los elementos de ambos conjuntos:
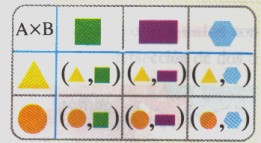
Estas combinaciones se pueden representar mediante pares ordenados, tal como se indican en la siguiente tabla.
Todo par ordenado escrito con números representa un punto del plano, donde la primera componente (el primer número) recibe el nombre de abscisa (eje x) y la segunda componente recibe el nombre de ordenada (eje y).
4.3 REPRESENTACIÓNCuando hablamos de par ordenado, nos estamos refiriendo a dos números, o figuras, encerrados en un paréntesis.
Su representación general es:
( a , b )
Respecto a esto, podemos preguntarnos ¿cómo se obtiene un par ordenado?, ¿para qué sirve un par ordenado?
Un par ordenado se puede obtener desarrollando una función o realizando la operación llamada producto cartesiano.
Como consecuencia, un par ordenado sirve para representar un subconjunto del producto cartesiano entre dos conjuntos, un punto en un plano cartesiano o bien una razón o una función.
4.2 PRODUCTO CARTESIANO
Cada par ordenado es una combinación entre elementos del conjunto A y elementos del conjunto B. Siempre el primer elemento pertenece al primer conjunto y el segundo elemento al segundo conjunto pero no al revés porque su representación no es conmutativa, es decir, no se puede alterar el orden.

Observa en el recuadro los conjuntos A y B y las combinaciones que se pueden hacer entre los elementos de ambos conjuntos:

Estas combinaciones se pueden representar mediante pares ordenados, tal como se indican en la siguiente tabla.
Todo par ordenado escrito con números representa un punto del plano, donde la primera componente (el primer número) recibe el nombre de abscisa (eje x) y la segunda componente recibe el nombre de ordenada (eje y).
A los pares
ordenados se los suele representar gráficamente es un sistema bidimensional, lo
cual trataremos con mayor profundidad más adelante.
4.4 RELACIONES
Cuando definimos
al producto cartesiano, se han relacionado a todos los elementos de un conjunto
con todos los elementos de otro conjunto. Nace el concepto de relación o
asociación.
Cuando a cada elemento de un conjunto le corresponde solo uno del otro, se habla de función.
Esto quiere decir que las funciones matemáticas siempre son, a su vez,
relaciones matemáticas, pero que las relaciones no siempre son
funciones.
En una relación matemática, al primer conjunto se lo conoce como dominio, mientras que el segundo conjunto recibe el nombre de rango o recorrido. Las relaciones matemáticas existentes entre ellos se pueden graficar en el esquema llamado plano cartesiano.
Supongamos que el dominio se llama M y el rango, N. Una relación matemática de M en N será un subconjunto del producto cartesiano M x N. Las relaciones, en otras palabras, serán pares ordenados que vinculen elementos de M con elementos de N.
Si M = {5, 7} y N = {3, 6, 8}, el producto cartesiano de M x N serán los siguientes pares ordenados:
M x N = {(5, 3), (5, 6), (5, 8), (7, 3), (7, 6), (7, 8)}
Con este producto cartesiano, se pueden definir diferentes relaciones. La relación matemática del conjunto de pares cuyo segundo elemento es menor a 7 es R = {(5, 3), (5, 6), (7, 3), (7, 6)}
Otra relación matemática que puede definirse es aquella del conjunto de pares cuyo segundo elemento es par: R = {(5, 6), (5, 8), (7, 6), (7, 8)}
Supongamos que el dominio se llama M y el rango, N. Una relación matemática de M en N será un subconjunto del producto cartesiano M x N. Las relaciones, en otras palabras, serán pares ordenados que vinculen elementos de M con elementos de N.
Si M = {5, 7} y N = {3, 6, 8}, el producto cartesiano de M x N serán los siguientes pares ordenados:
M x N = {(5, 3), (5, 6), (5, 8), (7, 3), (7, 6), (7, 8)}
Con este producto cartesiano, se pueden definir diferentes relaciones. La relación matemática del conjunto de pares cuyo segundo elemento es menor a 7 es R = {(5, 3), (5, 6), (7, 3), (7, 6)}
Otra relación matemática que puede definirse es aquella del conjunto de pares cuyo segundo elemento es par: R = {(5, 6), (5, 8), (7, 6), (7, 8)}
DOMINIO Y RANGO DE UNA RELACION
El dominio de una
relación es el conjunto de preimágenes; es decir, el conjunto formado por los
elementos del conjunto de partida que están relacionados.
Al conjunto de
imágenes, esto es, elementos del conjunto de llegada que están relacionados, se
le denomina recorrido o rango.
Ejemplo
Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R
la relación definida de A en B determinada por la regla “y es el doble de x” o
“y = 2x”, encontrar dominio y rango de la relación.
Solución
El total de pares ordenados que podemos
formar, o producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1,
8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3,
8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R
(y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de
2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen
de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el
Dominio y el conjunto de partida?
En el Dominio falta el elemento 1 del conjunto
de partida, por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de
llegada es elemento del rango? La respuesta es no, pues en el rango faltan el 5
y el 7.
REPRESENTACIÓN GRÁFICA DE LAS RELACIONES
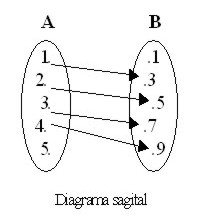
Los pares ordenados se pueden representar
gráficamente por medio de diagramas sagitales o por medio de puntos en el plano
cartesiano.
Veamos el
siguiente ejemplo.
Ejemplo
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y
R la relación definida por la regla
R = {(x, y) / y = 2x + 1}, graficar R.
Solución Los pares ordenados que pertenecen a
la relación (que cumplen con y = 2x + 1) son:
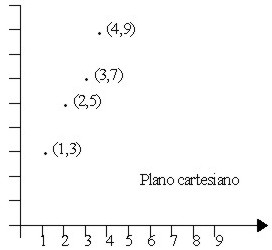
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la gráfica correspondiente es la siguiente:
|
No hay comentarios:
Publicar un comentario